Was ist die Monte-Carlo-Simulation?

Die Monte-Carlo-Simulation, auch bekannt als Monte-Carlo-Methode oder Mehrfachwahrscheinlichkeitssimulation, ist eine mathematische Technik, mit der die möglichen Ergebnisse eines ungewissen Ereignisses geschätzt werden können. Die Monte-Carlo-Methode wurde von John von Neumann und Stanislaw Ulam während des Zweiten Weltkriegs erfunden, um die Entscheidungsfindung unter ungewissen Bedingungen zu verbessern. Sie wurde nach einer bekannten Kasinostadt namens Monaco benannt, da das Element des Zufalls im Mittelpunkt des Modellierungsansatzes steht, ähnlich wie bei einem Roulettespiel.

Seit ihrer Einführung haben Monte-Carlo-Simulationen die Auswirkungen von Risiken in vielen realen Szenarien bewertet, z. B. in den Bereichen künstliche Intelligenz, Aktienkurse, Umsatzprognosen, Projektmanagement und Preisgestaltung. Sie bieten auch eine Reihe von Vorteilen gegenüber Prognosemodellen mit festen Eingaben, wie die Möglichkeit, Sensitivitätsanalysen durchzuführen oder die Korrelation von Eingaben zu berechnen. Die Sensitivitätsanalyse ermöglicht es Entscheidungsträgern, die Auswirkungen einzelner Inputs auf ein bestimmtes Ergebnis zu erkennen, und die Korrelation ermöglicht es ihnen, die Beziehungen zwischen beliebigen Inputvariablen zu verstehen.

Wie funktioniert die Monte-Carlo-Simulation?

Im Gegensatz zu einem normalen Prognosemodell sagt die Monte-Carlo-Simulation eine Reihe von Ergebnissen auf der Grundlage eines geschätzten Wertebereichs im Vergleich zu einer Reihe von festen Eingabewerten voraus. Mit anderen Worten: Eine Monte-Carlo-Simulation erstellt ein Modell möglicher Ergebnisse, indem sie eine Wahrscheinlichkeitsverteilung, z. B. eine Gleich- oder Normalverteilung, für jede Variable mit inhärenter Unsicherheit nutzt. Anschließend werden die Ergebnisse immer wieder neu berechnet, wobei jedes Mal ein anderer Satz von Zufallszahlen zwischen dem Mindest- und dem Höchstwert verwendet wird. Bei einem typischen Monte-Carlo-Experiment kann diese Übung Tausende von Malen wiederholt werden, um eine große Anzahl wahrscheinlicher Ergebnisse zu erhalten.

Monte-Carlo-Simulationen werden aufgrund ihrer Genauigkeit auch für langfristige Vorhersagen verwendet. Mit der Anzahl der Eingaben wächst auch die Anzahl der Vorhersagen, so dass Sie die Ergebnisse mit größerer Genauigkeit in die Zukunft projizieren können. Wenn eine Monte-Carlo-Simulation abgeschlossen ist, liefert sie eine Reihe möglicher Ergebnisse mit der Wahrscheinlichkeit, dass jedes Ergebnis eintritt.

Ein einfaches Beispiel für eine Monte-Carlo-Simulation ist die Berechnung der Wahrscheinlichkeit, mit der zwei Standardwürfel geworfen werden. Es gibt 36 Kombinationen von Würfelwürfen. Auf dieser Grundlage können Sie die Wahrscheinlichkeit für ein bestimmtes Ergebnis manuell berechnen. Mit einer Monte-Carlo-Simulation können Sie das Würfeln 10.000 Mal (oder öfter) simulieren, um genauere Vorhersagen zu erhalten.

Wie man die Monte-Carlo-Methoden einsetzt

Unabhängig davon, welches Tool Sie verwenden, umfassen Monte-Carlo-Verfahren drei grundlegende Schritte:

• Erstellen des Vorhersagemodells, wobei sowohl die abhängige Variable, die vorhergesagt werden soll, als auch die unabhängigen Variablen (auch als Eingabe-, Risiko- oder Vorhersagevariablen bezeichnet), die die Vorhersage beeinflussen, identifiziert werden.
• Festlegen der Wahrscheinlichkeitsverteilungen der unabhängigen Variablen. Verwenden Sie historische Daten und/oder das subjektive Urteil des Analysten, um einen Bereich wahrscheinlicher Werte zu definieren und jedem Wert eine Wahrscheinlichkeitsgewichtung zuzuweisen.
• Führen Sie wiederholt Simulationen durch und erzeugen Sie dabei Zufallswerte für die unabhängigen Variablen. Führen Sie dies so lange durch, bis Sie genügend Ergebnisse gesammelt haben, um eine repräsentative Stichprobe aus der nahezu unendlichen Anzahl möglicher Kombinationen zu bilden.

Sie können so viele Monte-Carlo-Simulationen durchführen, wie Sie möchten, indem Sie die zugrundeliegenden Parameter ändern, die Sie zur Simulation der Daten verwenden. Sie werden jedoch auch die Variationsbreite innerhalb einer Stichprobe berechnen wollen, indem Sie die Varianz und die Standardabweichung berechnen, die üblicherweise als Maß für die Streuung verwendet werden. Die Varianz einer bestimmten Variablen ist der erwartete Wert der quadrierten Differenz zwischen der Variablen und ihrem erwarteten Wert. Die Standardabweichung ist die Quadratwurzel der Varianz. In der Regel werden kleinere Varianzen als besser angesehen.

Illustration der Methode

Ein Servicetechniker betreut zwei Kunden. Kunde A benötigt mit einer Wahrscheinlichkeit von 20 Prozent die Unterstützung des Technikers, während Kunde B lediglich mit einer Wahrscheinlichkeit von 5 Prozent auf Hilfe angewiesen ist. Gesucht ist die Wahrscheinlichkeit, dass beide Kunden, die stochastisch unabhängig voneinander agieren, gleichzeitig den Servicetechniker um Hilfe bitten (die Lösung ist in diesem einfachen Fall auch analytisch ermittelbar, die Wahrscheinlichkeit eines gleichzeitigen Hilferufs beträgt 20 % * 5 % = 1 %).

Soll dieses Beispiel mit Hilfe der Monte-Carlo-Simulation gelöst werden, so wird zunächst eine zufällige Situation erzeugt und für diese geprüft, ob beide Kunden den Techniker um Hilfe bitten. Dies geschieht dadurch, dass zunächst Zufallszahlen für A und B ermittelt werden und jeweils gemäß der angegebenen Wahrscheinlichkeit ein Servicebedarf festgestellt wird. Da gängige Zufallszahlengeneratoren Zufallszahlen zwischen 0 und 1 generieren, kann die Zuordnung Servicebedarf erfolgen, wenn die Zufallszahl des Kunden A kleiner als 0,2 und die des Kunden B kleiner als 0,05 ist. Anschließend ist die Zielgröße der Simulation zu ermitteln, was im vorliegenden Fall bedeutet, dass beide Kunden gleichzeitig einen Servicebedarf (beziehungsweise keinen gleichzeitigen Servicebedarf) anmelden.

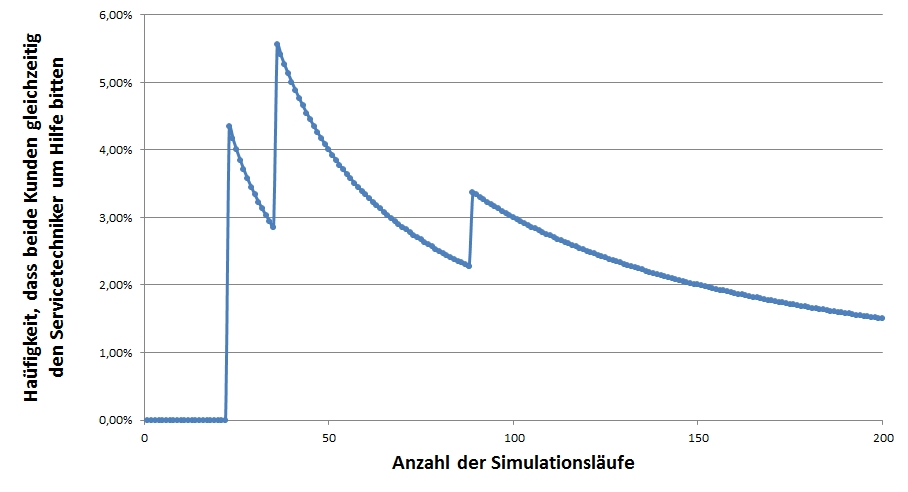
Diese Abfolge der Schritte 1 und 2 wird nun so lange wiederholt, bis die sich ergebende Verteilung der Zielgröße eine stabile Verteilung zeigt. Wie aus nachfolgender Abbildung ersichtlich, konvergiert die Zielgröße mit steigender Anzahl an Simulationsläufen gegen den bereits analytisch ermittelten Wert von 1 Prozent.

Literatur:

RiskNet