im Toleranzmanagement für die Beschreibung von Form und/oder Lageeigenschaften.
Um in den verschiedenen Toleranzsimulationssoftwaren die Streuung der Längen- und/oder Zweipunktmasse abzubilden werden, zum Nennwert auch die erwartete Verteilungsfunktion angegeben, welche aus Erfahrungswerten der Industrie gebildet wurden.

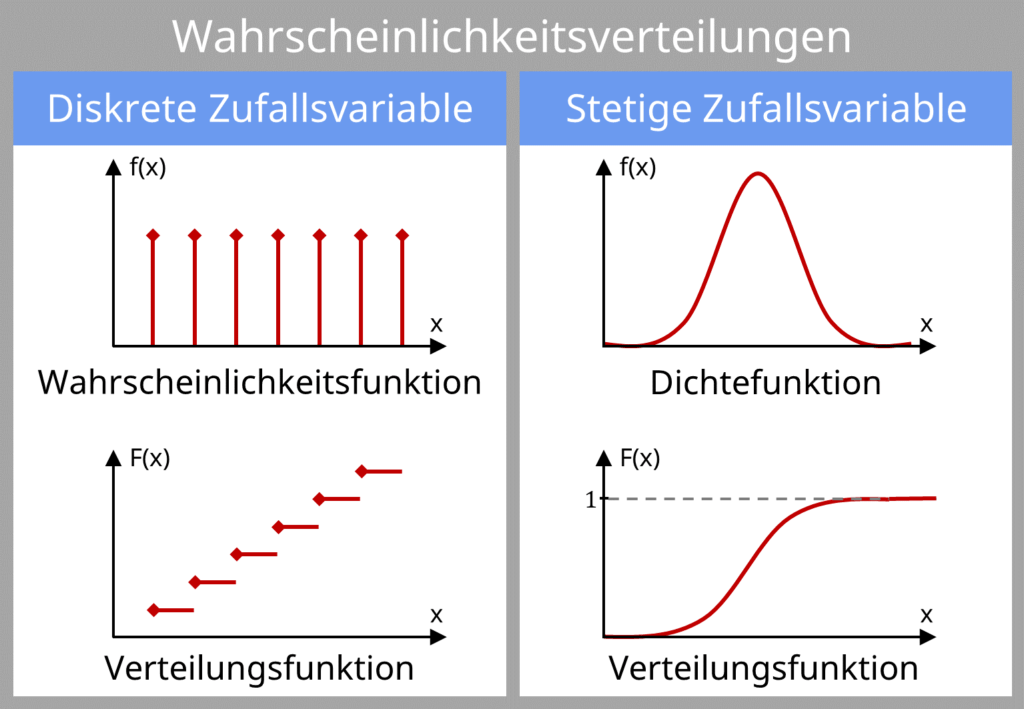
Es handelt sich immer um stetige Zufallsvariable, welche als Wahrscheinlichkeitsverteilung sich in eine Dichtefunktion darstellen.
kurze Beschreibung der verschiedenen Typen
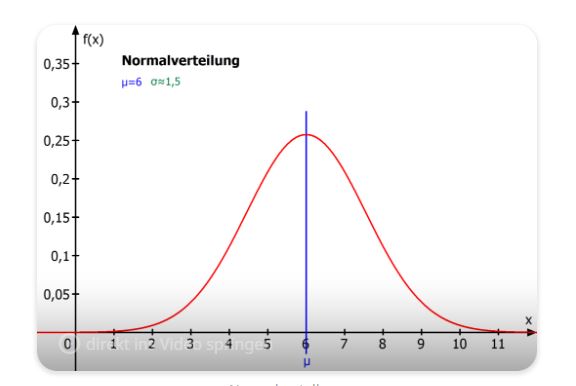
Normalverteilung
Die Normalverteilung verwendest du, um Häufigkeiten von Daten und Beobachtungen darzustellen. Du nennst die Normalverteilung auch Gaußverteilung (nach dem deutschen Mathematiker Carl Friedrich Gauß) oder Glockenkurve — entsprechend dem typischen Verlauf der Normalverteilung.
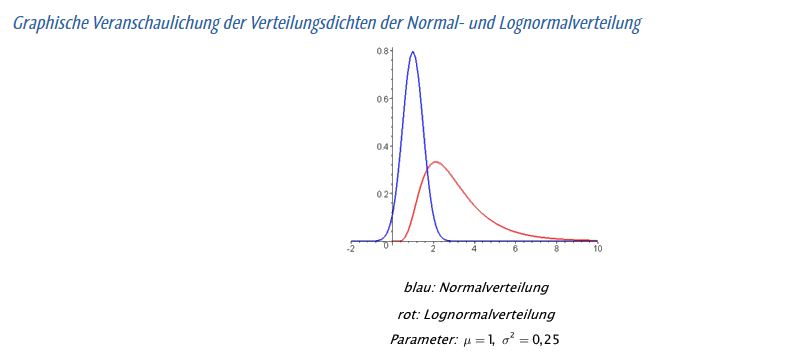
Logarithmische Normalverteilung
Die logarithmische Normalverteilung (kurz LNV) lässt sich aus der Gaußschen Fehlerfunktion (lineare Normalverteilung) ableiten durch Substitution, denn der Logarithmus der Partikelgröße (ln x) ist meist normal verteilt.
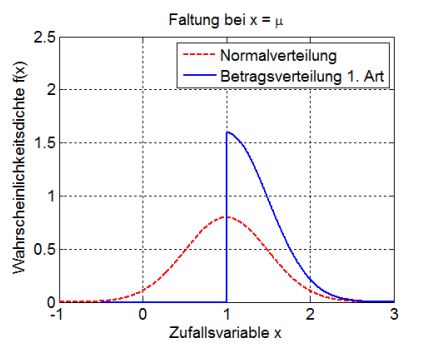
Betragsnormalverteilung 1 Art
Wird die Normalverteilung an einem beliebigen Punkt unterhalb des Mittelwertes μ gefaltet, führt dies zur Betragsverteilung 1. Art. Durch die Faltung werden die Werte links des Faltungspunktes denen rechts vom Faltungspunkt additiv überlagert. Dabei entsteht die Wahrscheinlichkeitsdichte f(x) der Betragsverteilung 1. Art zu
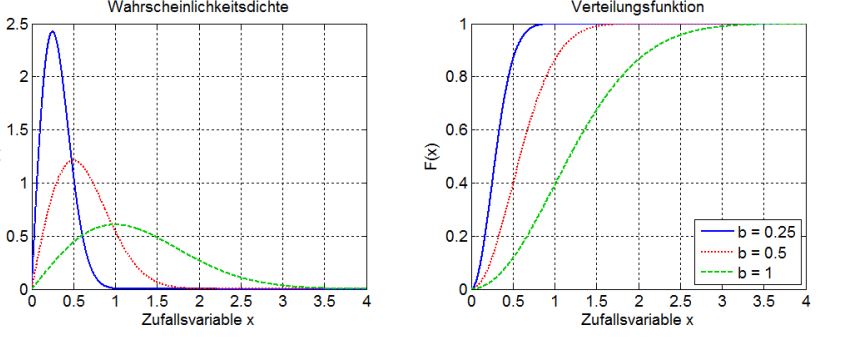
Betragsnormalverteilung 2 Art
Die Rayleigh-Verteilung oder Betragsverteilung 2. Art ist eine zweidimensionale Verteilung, die dann eingesetzt wird, wenn sich ein Merkmal aus zwei Komponenten zusammensetzt, wobei die Streuung der Einzelkomponenten als gleich angesehen werden kann. Anwendung findet die Betragsverteilung 2. Mithilfe der Rayleigh-Verteilung wird die Verteilung des Betrages zweier unabhängiger normalverteilter Zufallsgrößen mit der Standardabweichung σ = b beschrieben
Rechteckverteilung
Die stetige Gleichverteilung, auch Rechteckverteilung, kontinuierliche Gleichverteilung, oder Uniformverteilung genannt, ist eine stetige Wahrscheinlichkeitsverteilung. Sie hat auf einem Intervall {\displaystyle [a,b]}

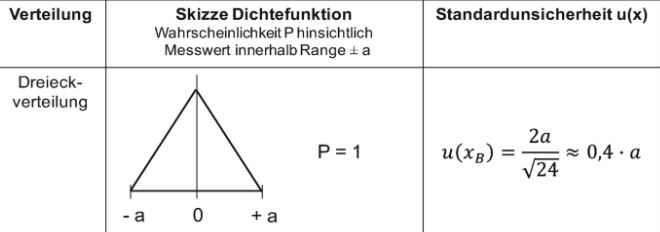
Dreiecksverteilung
Liegen nur sehr wenige konkrete Daten zur Bestimmung der Verteilungsfunktion f(x) einer Zufallsvariablen x vor, wird in der Praxis die Dreiecksverteilung als erste Schätzung verwendet. Die Dreiecksverteilung ist auch als Simpson-Verteilung bekannt.

Hinterlasse einen Kommentar