auch t- Verteilung genannt ist für die Betrachtung kleiner Stichproben besser geeignet als die Normalverteilung.
Bei beobachteten Größen mit geringer Datenmenge (nw < 20) wird die Student-Verteilung verwendet. Sie hängt u. a. von der Anzahl der Freiheitsgrade nf (nf = nw −1) ab. Für nf => ∞ geht die Student-Verteilung in die Normalverteilung über. Die Gleichung zur Berechnung der Funktionswerte für die Dichte der Student-Verteilung lautet
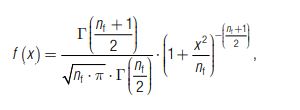
mit der Gamma-Funktion ![]()
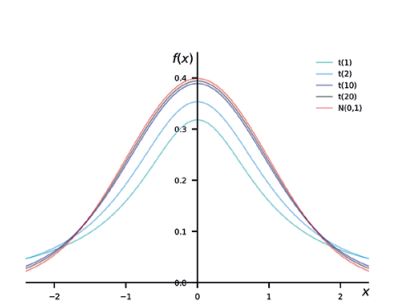
In der Abbildung sind für die Freiheitsgrade nf = 1, 2, 10, und 20 die entsprechenden Kurvenverläufe der Dichtefunktion der Student-Verteilung t (1), t (2), t (10), t (20) und zusätzlich zum Vergleich der Kurvenverlauf der Dichtefunktion der Normalverteilung N (0, 1) eingetragen.
Die Abweichungen zwischen der Student-Funktion und der Normalverteilung werden durch den Student-Faktor t beschrieben. In der Tabelle sind die Student-Faktoren für eine Überdeckungswahrscheinlichkeit von 68,3 % (= 1 s) zusammengestellt.
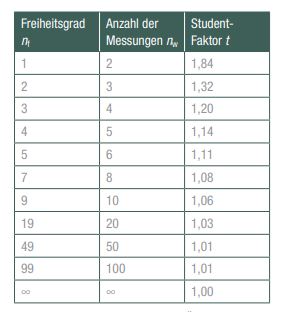
Der Student-Faktor t kann als Faktor betrachtet werden, mit dem z. B. eine empirische Standardabweichung (für nw > 20) zu multiplizieren ist, um die gleiche Überdeckungswahrscheinlichkeit zu erhalten wie für die Normalverteilung. Mit der Student-Verteilung werden ebenfalls bei der Berechnung der Messunsicherheit nach GUM Einflussgrößen vom Typ A bewertet. Der Gewichtsfaktor beträgt, wie bei der Normalverteilung, ebenfalls G = 1.
Weitere Hinweise zur Student-Verteilung können der Fachliteratur entnommen werden, wie z.B. /Höpcke 1980, S. 182 f./, /Niemeier
2002, S. 86 ff./ und /Pesch 2010, S. 33 ff/ oder auch Keferstein 2021.

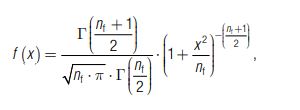
Hinterlasse einen Kommentar